For å benytte veiledet maskinlæring, trenger vi to ting;
- et sett med variabler (input)
- en variabel vi ønsker å predikere (output)
Ved hjelp av en algoritme, kan mappingfunksjonen mellom input-variablene og output-variabelen læres. Målet er å kunne predikere en output-variabel gitt et sett med input-variabler. Uansett hvilken metode vi bruker, vil aldri samtlige prediksjoner være korrekte. Det vil alltid være en prediksjonsfeil (error) tilstede. Denne splittes ofte i tre deler; “bias error”, “variance error” og “irreducible error”.
Bias error
“Bias error” kommer av forenklingene algoritmen vi benytter tar for å gjøre mappingfunksjonen lettere å lære. Høy “bias error” kan føre til at mappingfunksjonen overser viktige sammenhenger mellom input-variablene og output-variabelen. Det kaller vi “underfitting”.
Variance error
“Variance error” sier noe om hvor forskjellig den predikerte output-variabelen ville vært dersom et annet datasett ble benyttet under trening av modellen. Høy “variance error” kan føre til at mappingfunksjonen modellerer støyen i treningsdataene, og ikke de faktiske sammenhengene. Vi snakker da om “overfitting”.
Irreducible error
“Irreducible error” er knyttet til utformingen av problemet, og kan skyldes ukjente variabler og støy. Denne typen feil kan ikke reduseres, uavhengig av hvilken algoritme som benyttes.
Vi kan påvirke “bias error” og “variance error”, men ikke “irreducible error”. Ideelt sett ønsker vi en mappingfunksjon med lav “bias error” og lav “variance error”, men dessverre er ikke det så enkelt å få til. “Bias error” og “variance error” henger sammen, så ved å redusere en av de, vil den andre øke. Vi må derfor finne en balanse mellom disse vi kan akseptere. Figur 1 visualiserer de ulike kombinasjonene av høy og lav “bias error” og “variance error”.
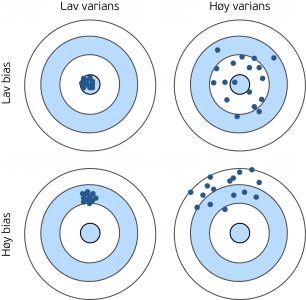
Når vi har kommet frem til en mappingfunksjon, og ser at den ikke presterer så godt som vi ønsker, er det flere ting vi kan gjøre. Hvilke feilreduserende tiltak som vil kunne fungere, er helt avhengig av hvilken type feil vi ønsker å redusere. Det finnes flere metoder for å identifisere om det er “bias error” eller “variance error” som fører til upresise prediksjoner, men disse beskriver vi ikke her. La oss heller se på mulige tiltak.
Les mer:
Utvide datasettet
Et alternativ er å skaffe flere treningsdata. Ved å benytte et større datasett for å trene opp mappingfunksjonen, vil problemet med “overfitting” reduseres. Mappingfunksjonen vil måtte ta hensyn til flere data, og dermed vil den predikere mindre av støyen, og mer av de faktiske sammenhengene.
Endre antall input-variabler
Et annet tiltak som kan bidra til å redusere “variance error”, er å redusere antall input-variabler. Dersom noen av variablene har liten innvirkning på mappingfunksjonen, kan vi vurdere å utelate disse. Det samme gjelder dersom enkelte input-variabler er korrelerte.
Ofte har vi mulighet til å legge til flere input-variabler, eller splitte opp noen av de vi allerede har. Det vil kunne bidra til å redusere “bias error”. For eksempel, hvis vi har en input-variabel som inneholder både kjønn og alder, kan vi erstatte denne med en variabel som inneholder kjønn, og en som inneholder alder.
Legge til polynom-variabler
For å redusere “underfitting”, altså “bias error”, kan vi legge til polynomer av input-variablene vi allerede har. For eksempel, hvis x1 og x2 er to av input-variablene, kan vi legge til ledd som x12, x1x2, x12x24 osv. Her må vi være oppmerksom på at “for mange” polynom-ledd fort kan gi et “overfitting”-problem.
Endre regulariseringsparameteren
Regulariseringsparameteren, ofte angitt som λ, er en parameter som brukes for å styre hvor mye vi skal redusere “overfitting” i et maskinlæringsproblem. Ved å velge en høy λ-verdi, reduseres graden av “overfitting”, som igjen reduserer variansen i de estimerte parameterne i mappingfunksjonen. Ulempen er at høye λ-verdier gir økt “bias error”, altså kan viktige sammenhenger mellom input-variablene og output-variabelen bli oversett.
Tabell 1 viser en oppsummering av tiltakene vi har nevnt.
| Reduserer “bias error” | Reduserer “variance error” | |
|---|---|---|
| Skaffe flere treningsdata | ||
| Redusere antall input-variabler | ||
| Øke antall input-variabler | ||
| Legge til polynom-variabler | ||
| Redusere regulariseringsparameteren | ||
| Øke regulariseringsparameteren |
Tabell 1: Oversikt over hvilke tiltak som kan bidra til å redusere hvilke typer feil.
Konklusjon
Dersom mappingfunksjonen vår ikke gir de resultatene vi ønsker, finnes det altså flere mulige tiltak, men de vil ikke nødvendigvis gi oss de forbedringene vi er ute etter. Dersom vi har et “underfitting”-problem, vil det ikke hjelpe å utvide treningsdatasettet vårt. Tilsvarende vil det ikke hjelpe å legge til flere input-variabler dersom problemet er høy “variance error”. Det er derfor avgjørende å kjenne til hvilken type feil vi ønsker å redusere før vi ukritisk øker datamengden, endrer på input-variabler eller justerer regulariseringsparameteren.
Høres dette interessant ut? Ta gjerne kontakt for en uforpliktende prat.
Kontakt oss på visma.no/consulting

